»Fluchtwege«
Bilder von "Z-Bahnen" der Mandelbrot-Iteration Z→Z²+C
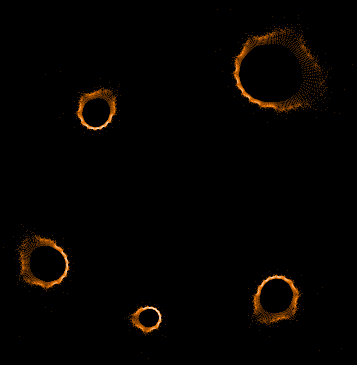
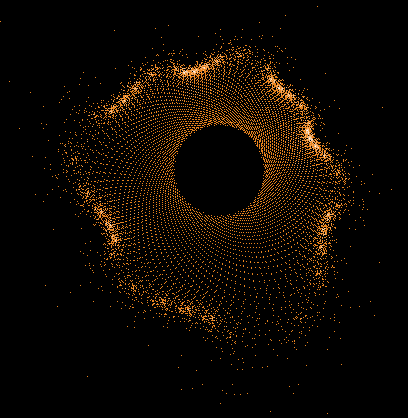
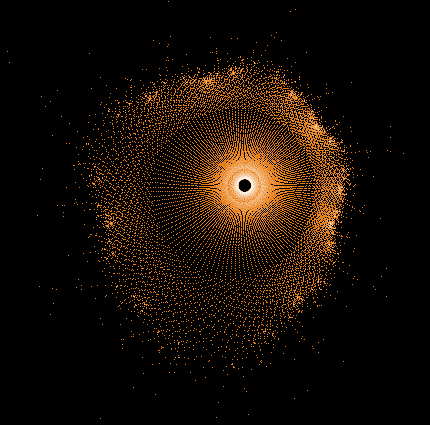
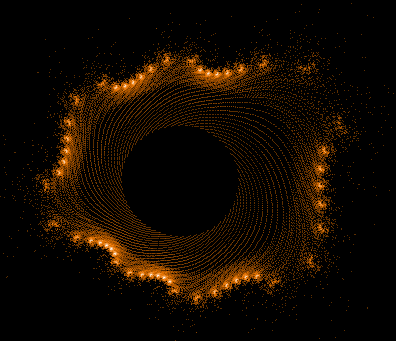
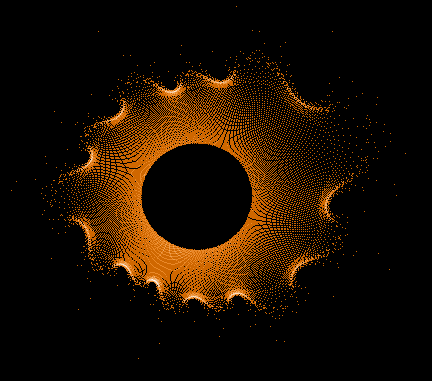
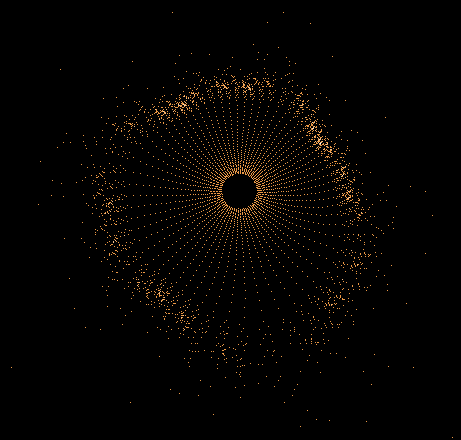
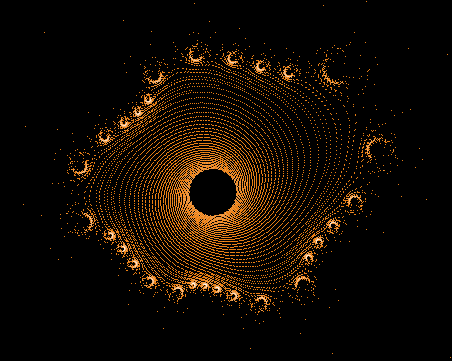
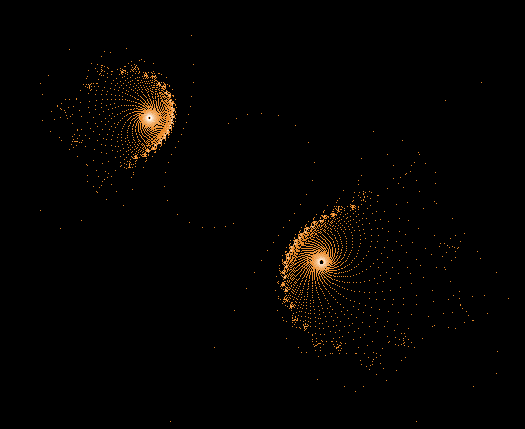
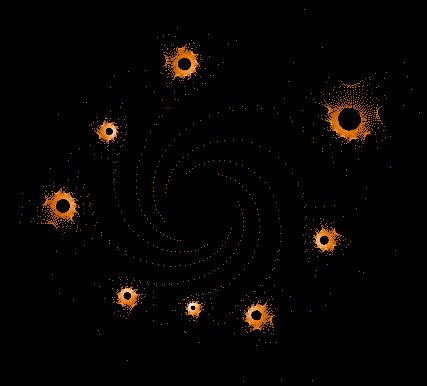
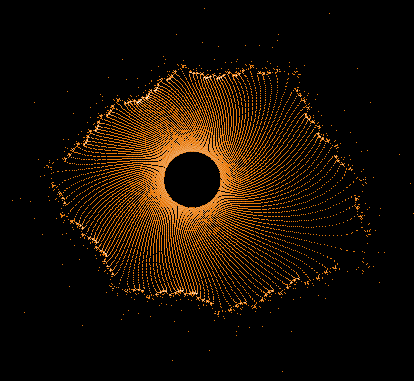
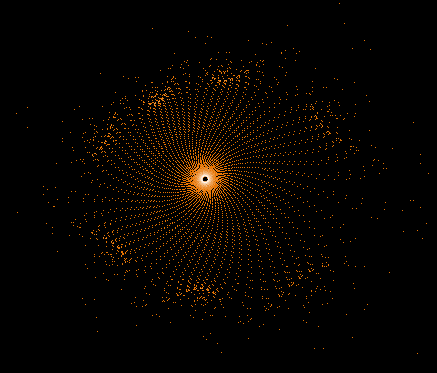
Während der Mandelbrot-Iteration Z→Z²+C „hüpft“ die Zahl Z auf der Komplexen Zahlenebene umher und erzeugt dabei interessante Muster. Hier einige Beispiele einzelner "Bahnen" der Zahl Z sowie auch Überlagerungen sehr vieler »Z-Bahnen«, die dann wieder die vertraute Grundstruktur des »Apfelmännchens« erkennen lassen, jedoch auf eine ganz neue Art.
Die folgenden Bilder von "Z-Bahnen" wurden mit dem Z-Orbit-Plotter erzeugt. Diese JavaScript-Anwendung berechnet für eine hohe Anzahl (z.B. 1 Million bis 1 Milliarde) zufälliger Startpunkte C mittels der Mandelbrot-Iteration Z→Z²+C eine Folge von Z-Zahlen und zeichnet diese auf das Bild. Es werden jedoch nur diejenigen Z-Bahnen gezeichnet, die divergieren, also nach "unendlich" abhauen (daher der Titel "Fluchtwege"). Weitere Erklärungen zu "Z-Bahnen" und zur JavaScript-Anwendung befinden sich in dem englischsprachigen Artikel Mandelbrot Z Orbits.
Diese Galerie besteht aus mehreren Bildserien. Jede Serie beginnt mit einem großen Gesamtbild, in dem alle vom Programm ermittelten Z-Bahnen kombiniert sind. Darunter folgen einzelne ausgewählte Z-Bahnen aus dem Gesamtbild.
- Serie 7 -
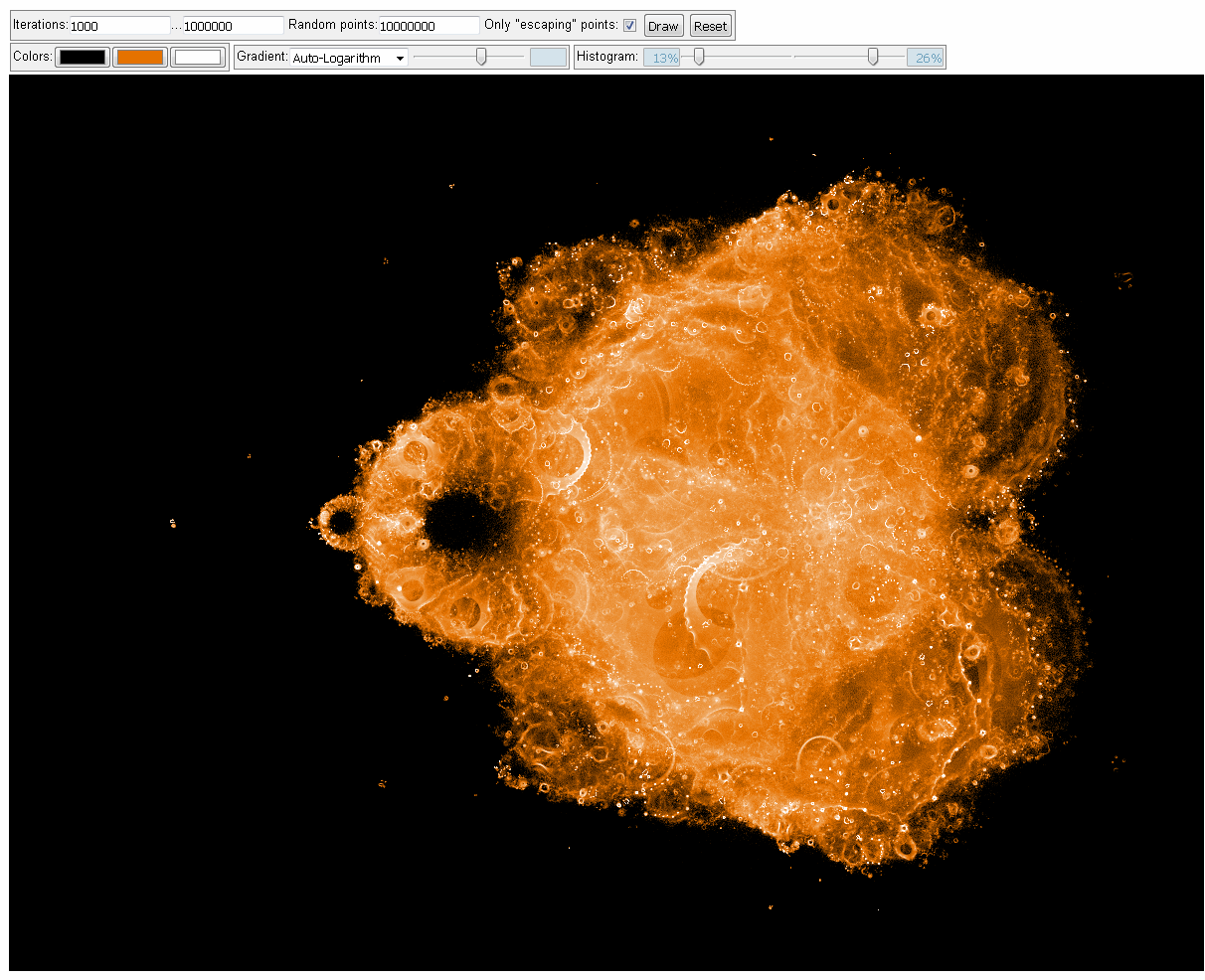
0...1.000 Iterationen, 1.000.000.000 Z-Bahnen
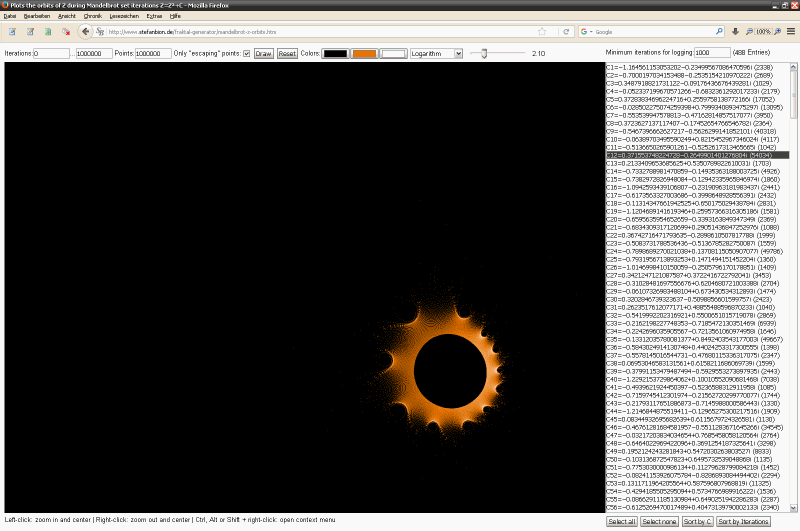
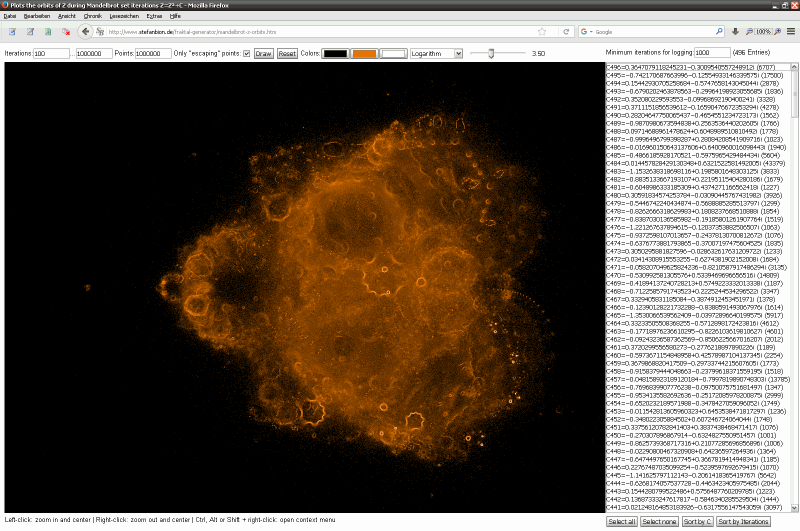
Screenshot der Anwendung
- Serie 6 -
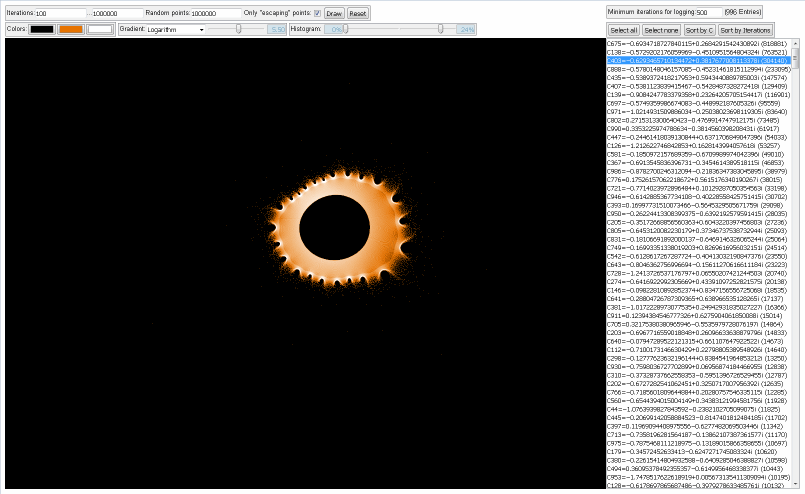
1.000...1.000.000 Iterationen, 10.000.000 Z-Bahnen
Screenshot der Anwendung
- Serie 5 -
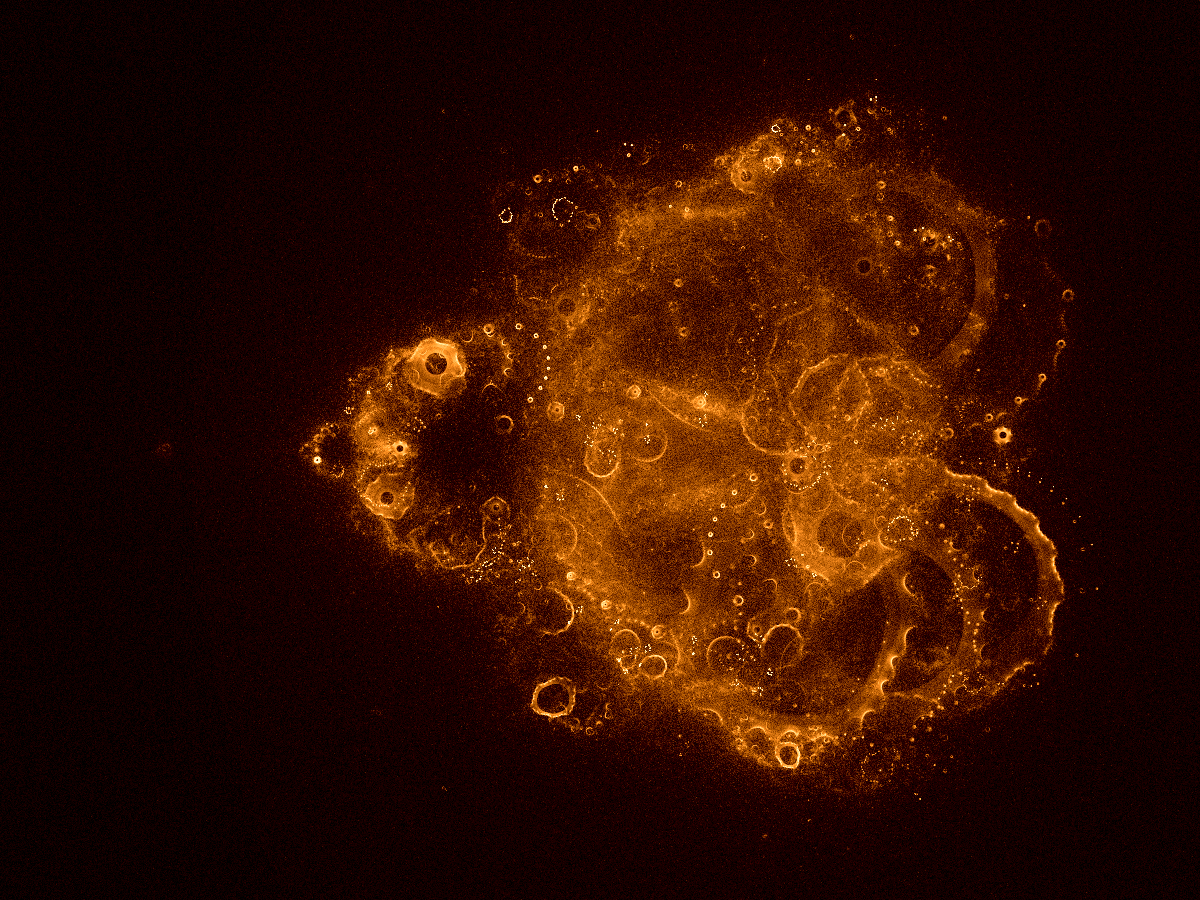
100...1.000.000 Iterationen, 1.000.000 Z-Bahnen
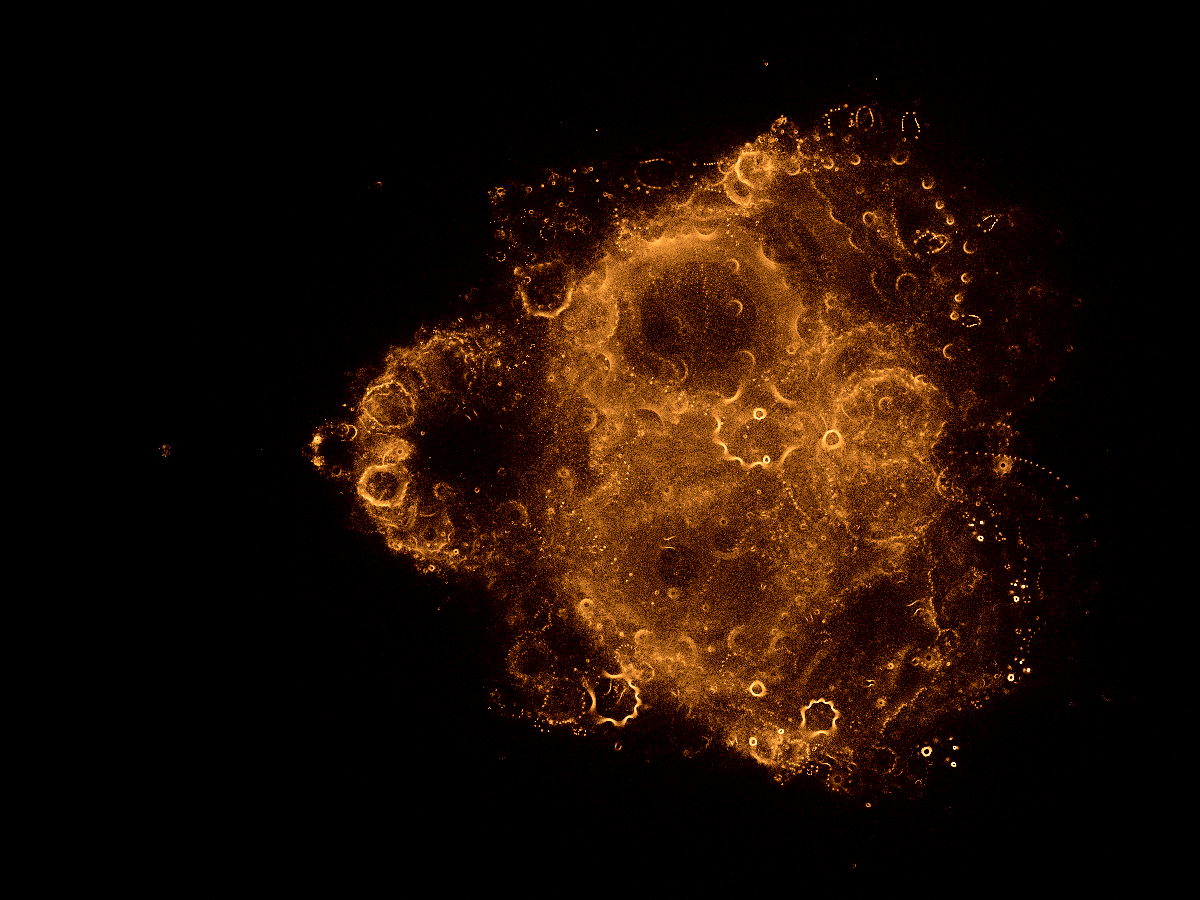
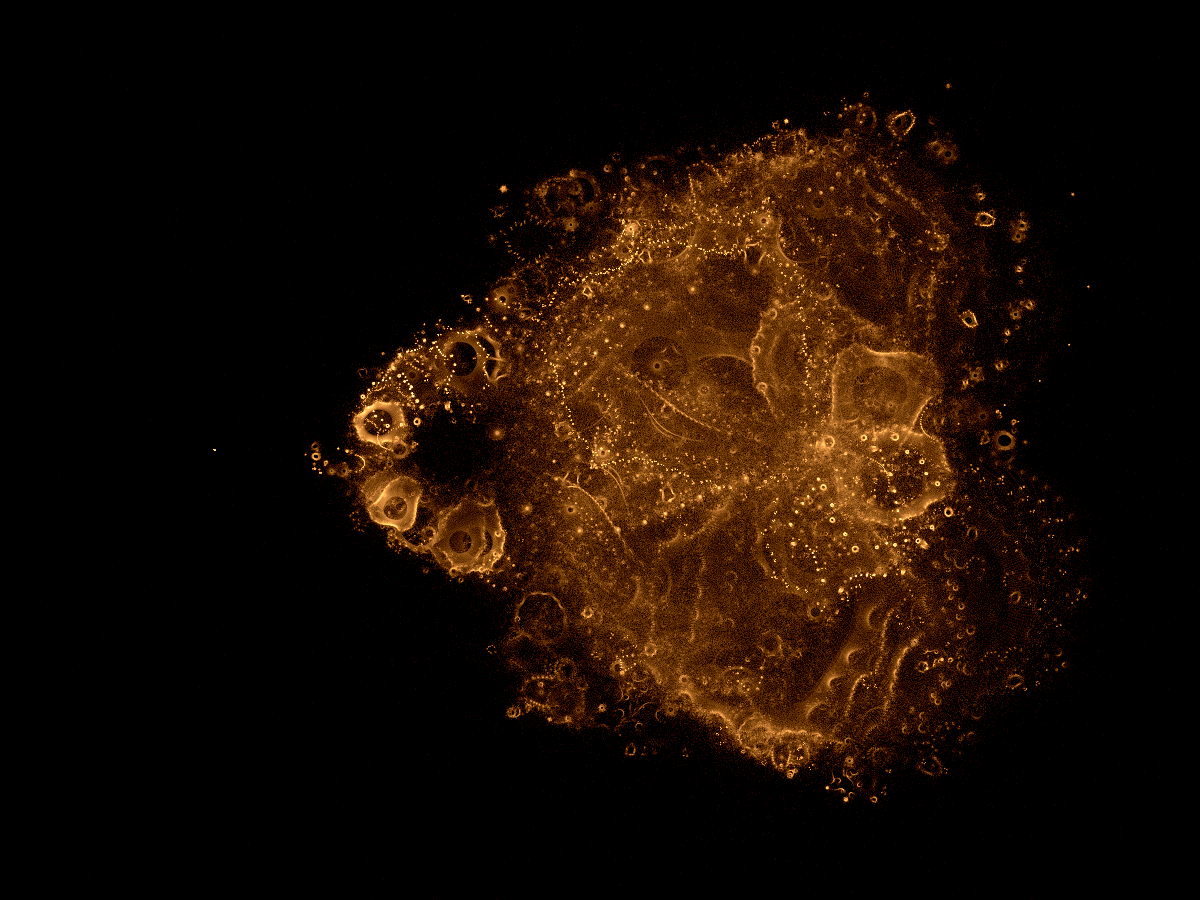
Gesamtbild (original, unbearbeitet)
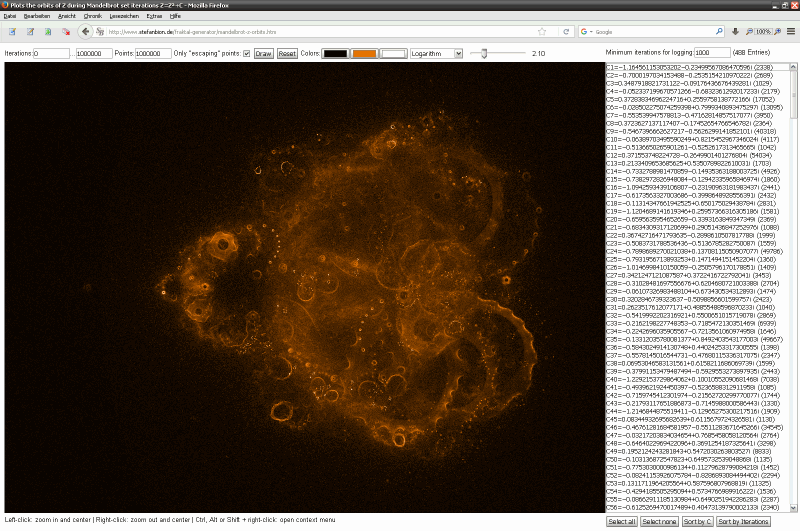
Screenshots der Anwendung
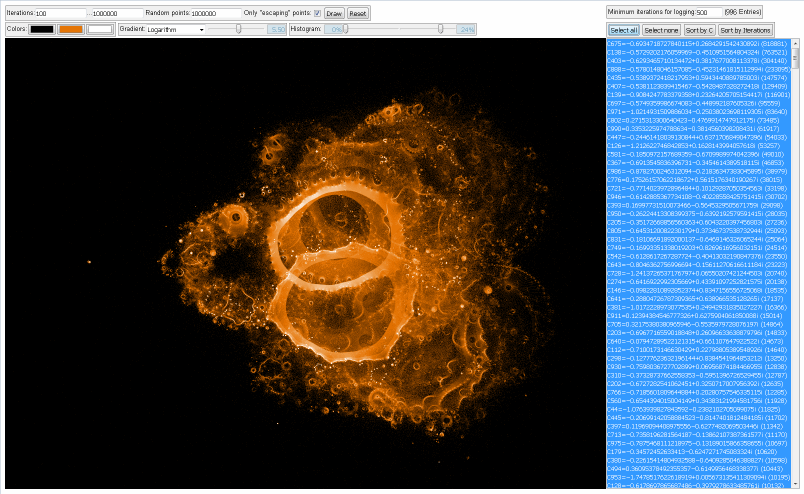
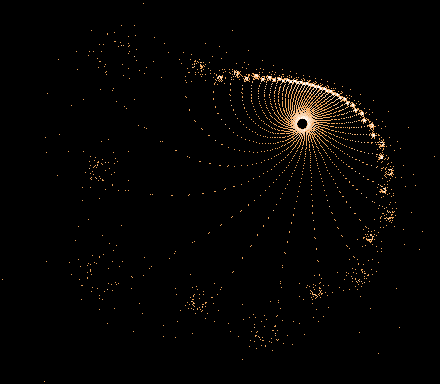
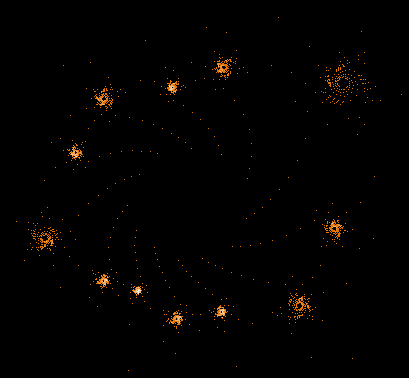
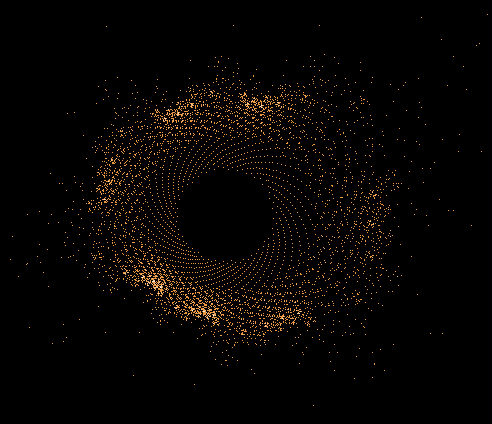
Einige einzelne Z-Bahnen aus obigen Gesamtbild
Die nächsten drei Bilder zeigen die 3 längsten Z-Bahnen: C675 (818881 Iterationen), C138 (763521 Iterationen) and C403 (304140 Iterationen). Diese sind auch in dem Gesamtbild gut zu erkennen.



- Serie 4 -
100...1.000.000 Iterationen, 1.000.000 Z-Bahnen
Gesamtbild (Histogramm verbessert)
Screenshots der Anwendung
Einige einzelne Z-Bahnen aus obigen Gesamtbild
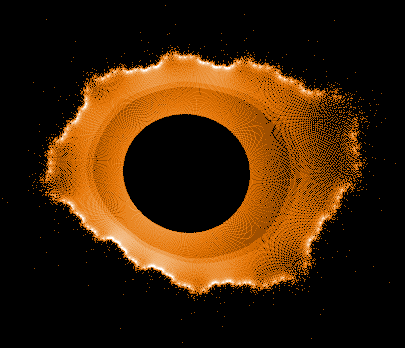

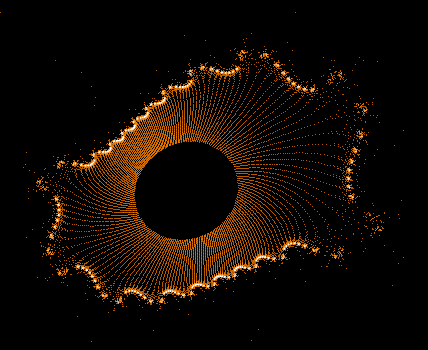
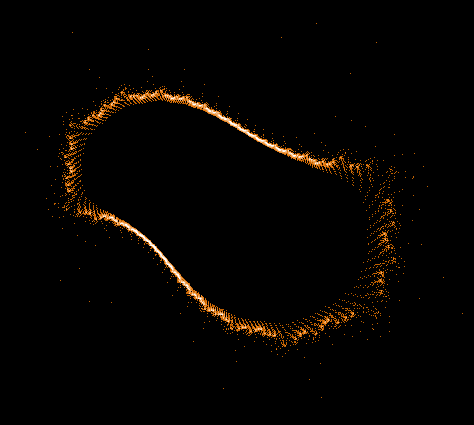
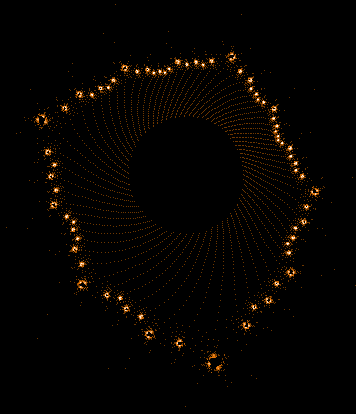

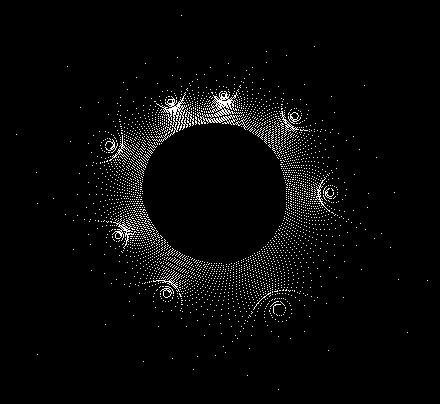
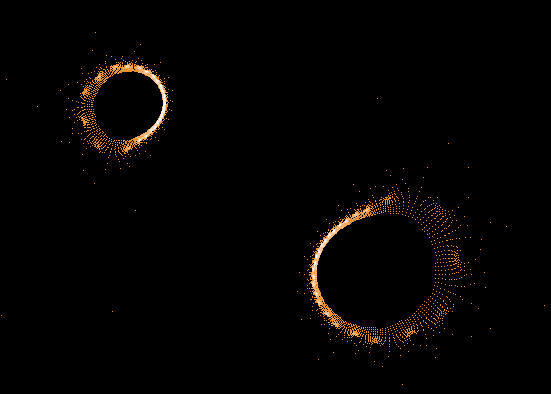

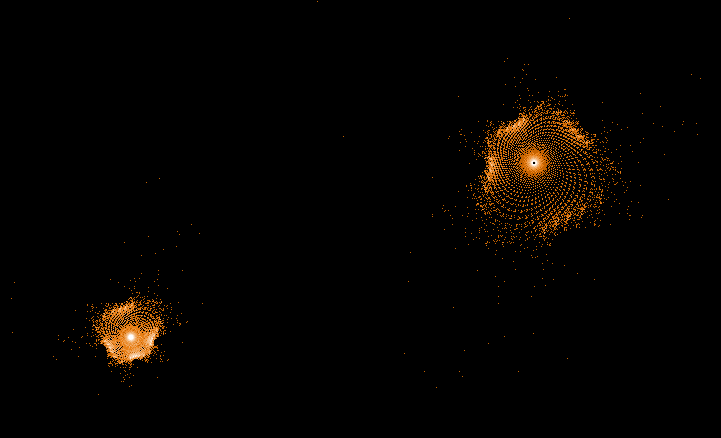
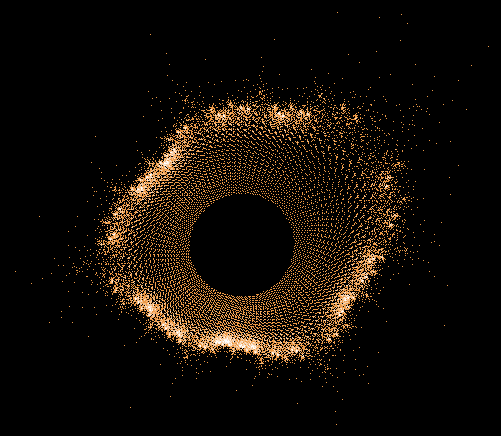
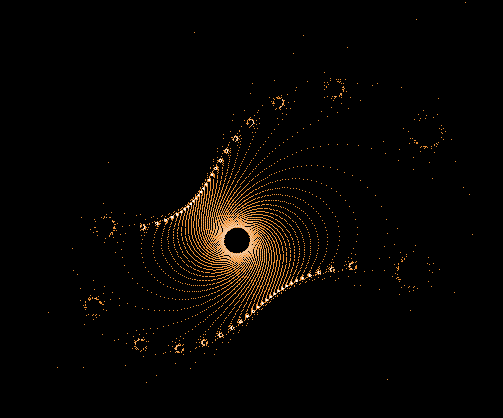



- Serie 3 -
100...1.000.000 Iterationen, 1.000.000 Z-Bahnen
Gesamtbild (Histogramm verbessert)
Screenshots der Anwendung
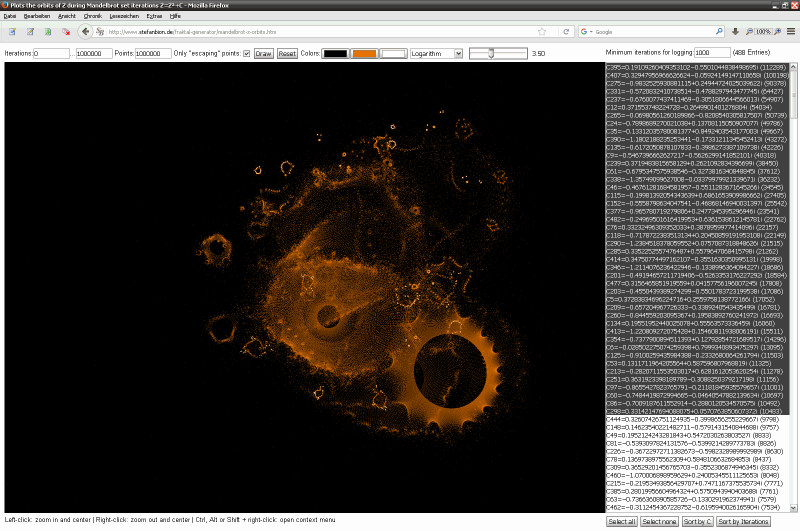
Einige einzelne Z-Bahnen aus obigen Gesamtbild

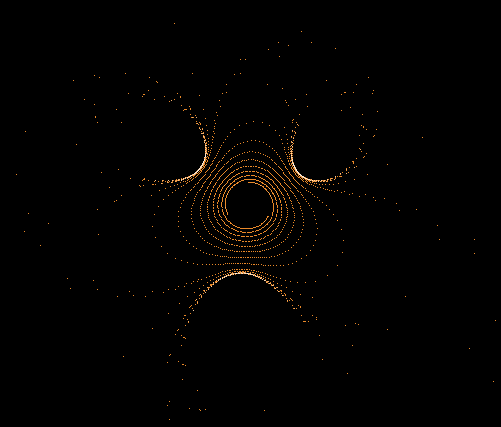


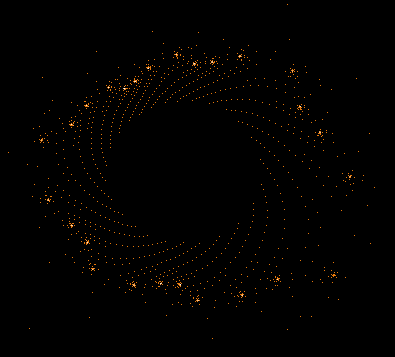
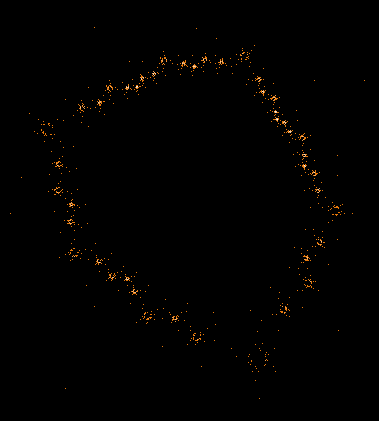
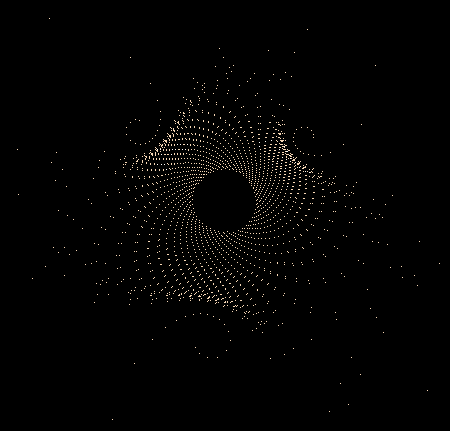
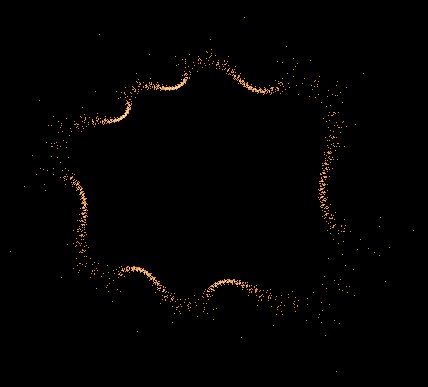
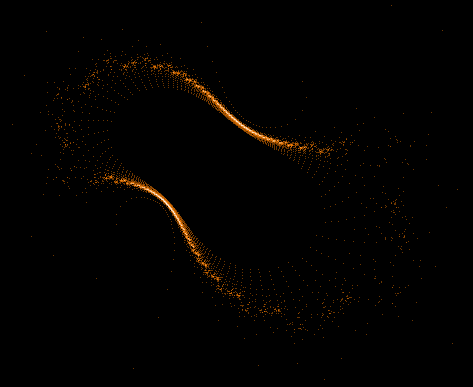

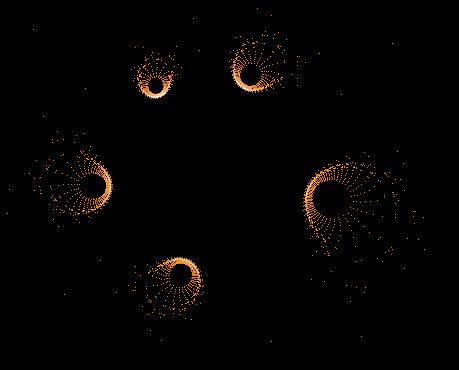
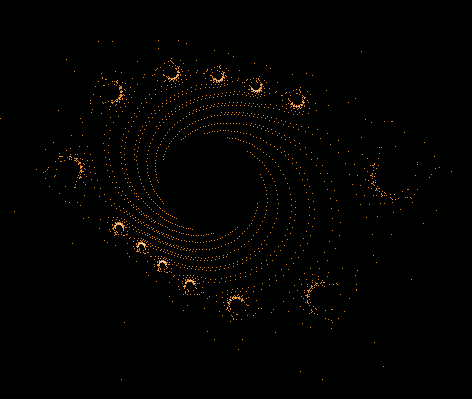


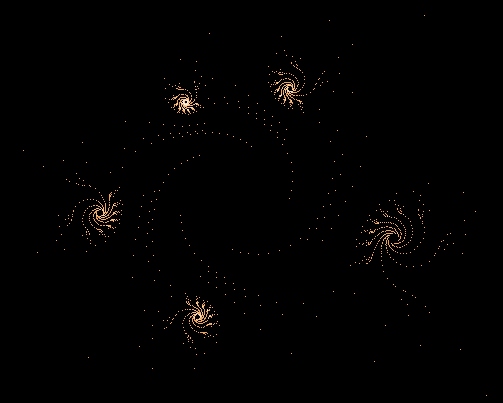



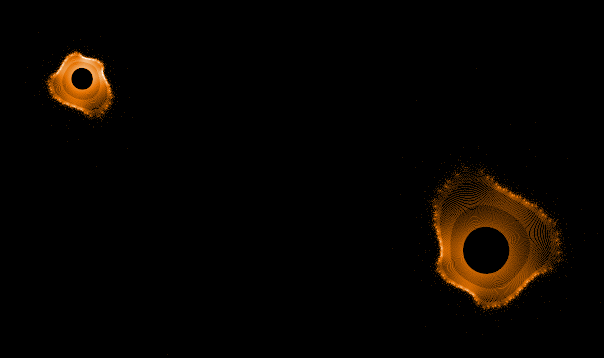
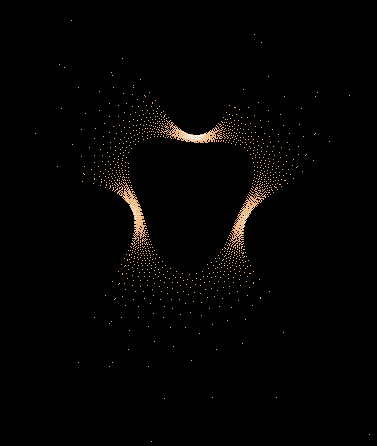

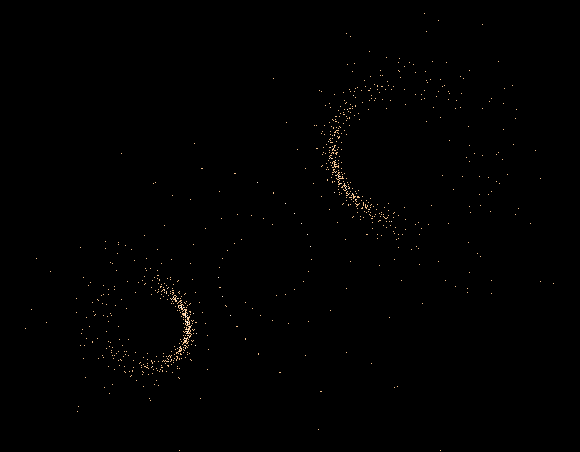

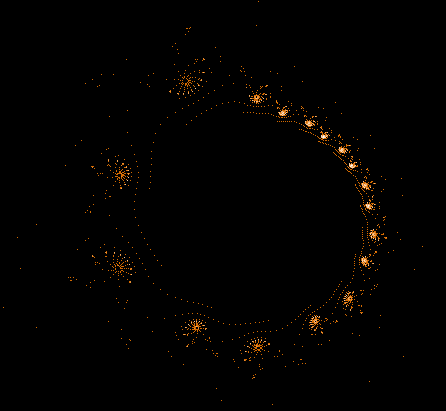
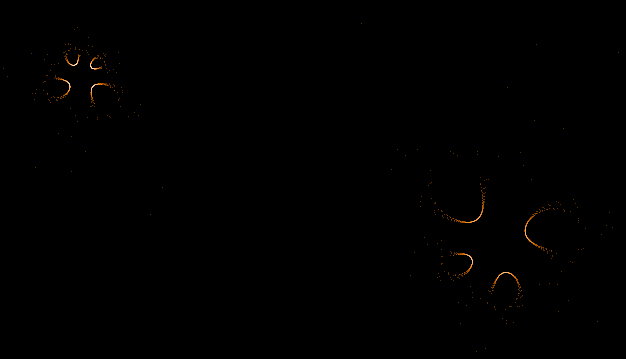
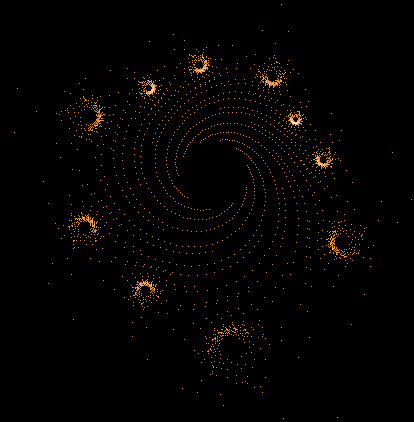

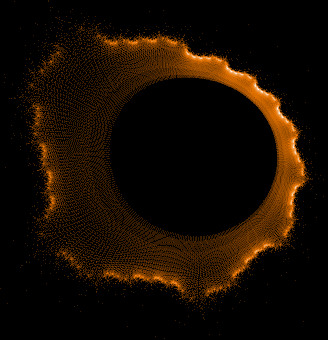

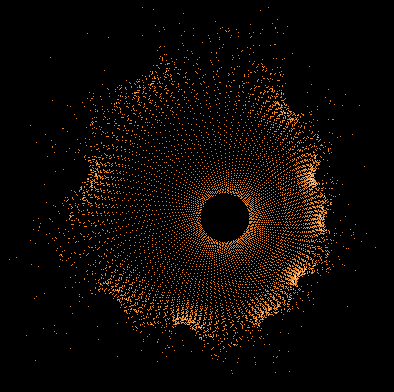
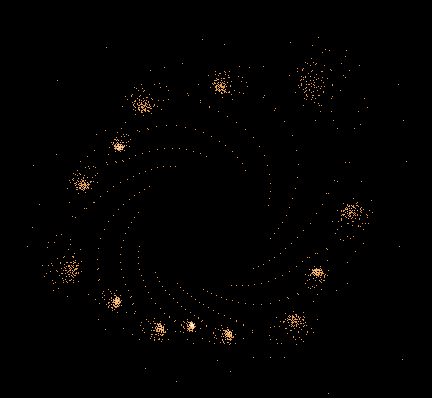
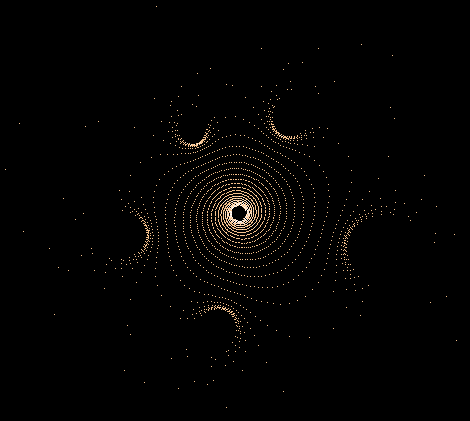
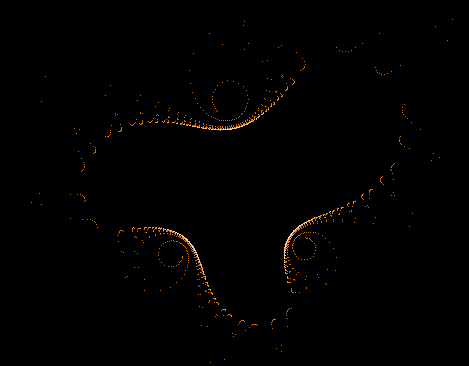
- Serie 2 -
0...1.000.000 Iterationen, 1.000.000 Z-Bahnen
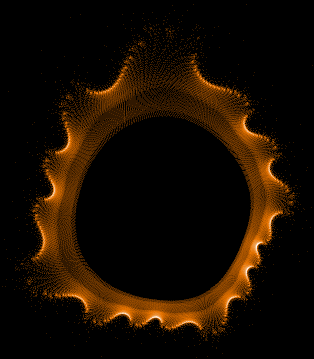
Gesamtbild (Histogramm verbessert)
Screenshots der Anwendung
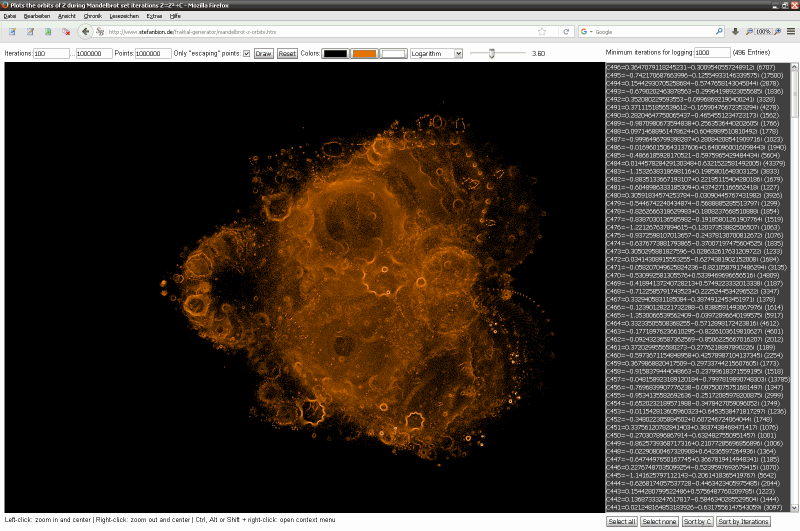
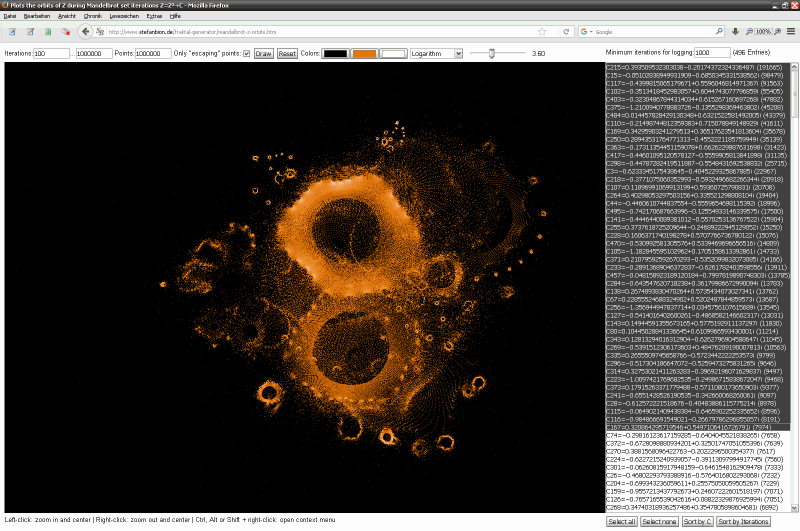
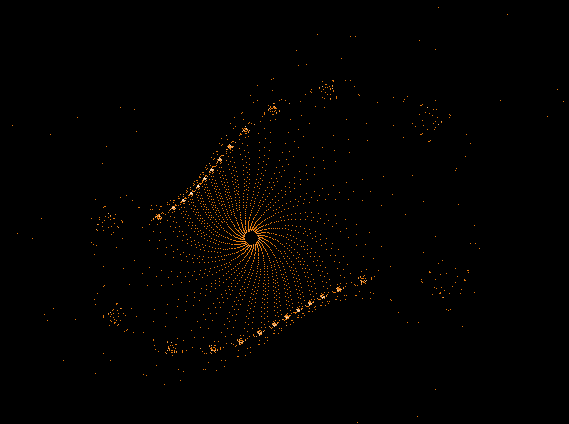
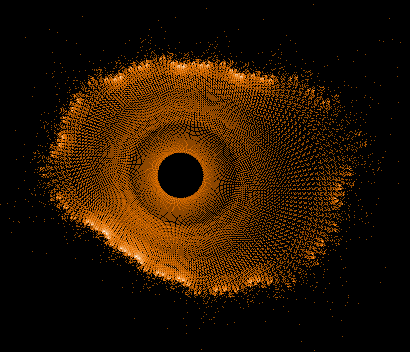
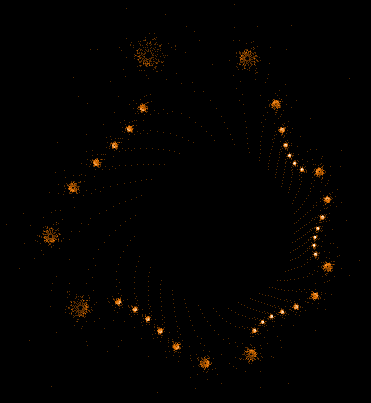
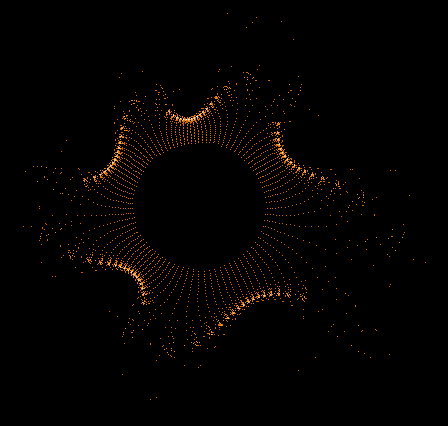
Einige einzelne Z-Bahnen aus obigen Gesamtbild
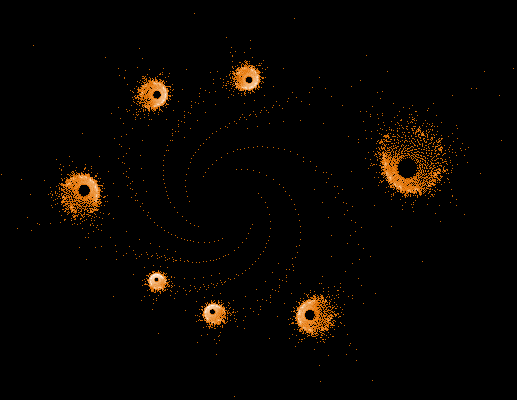
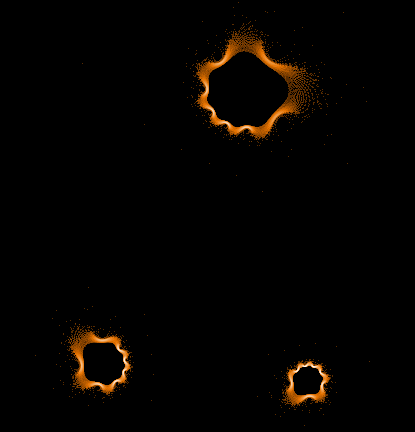

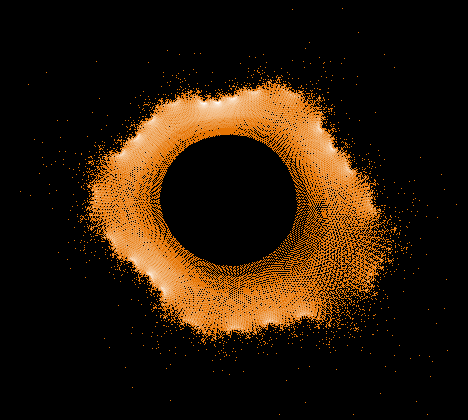
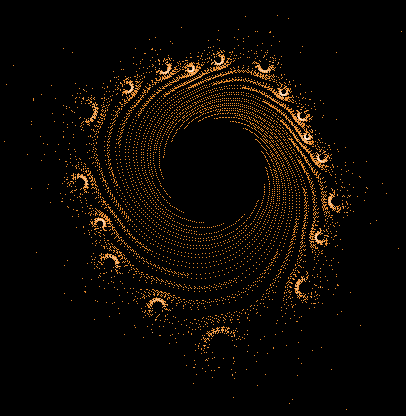
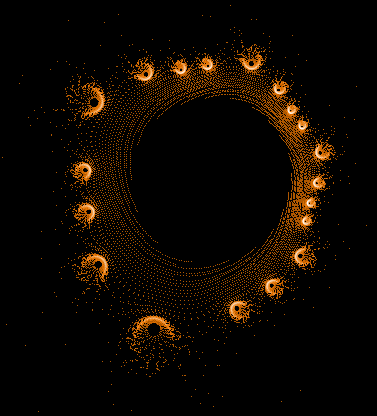

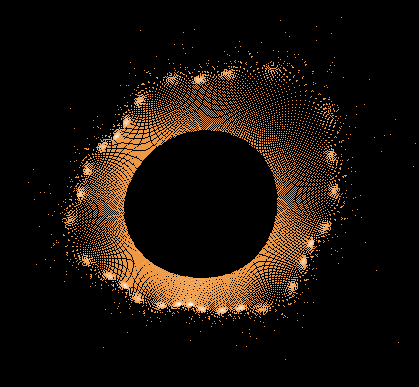
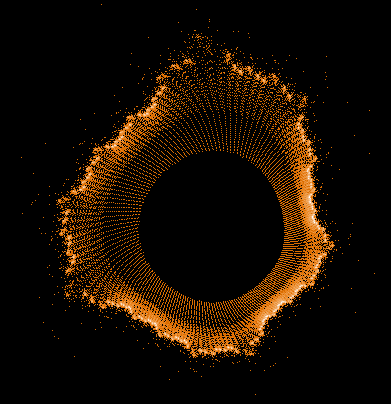
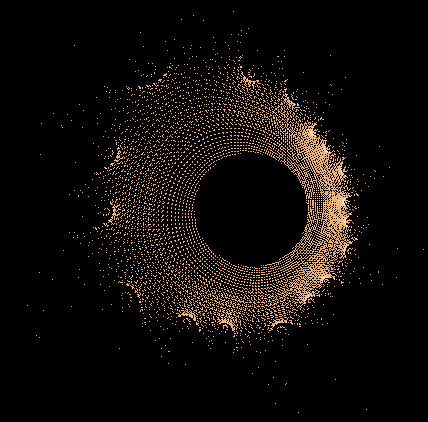
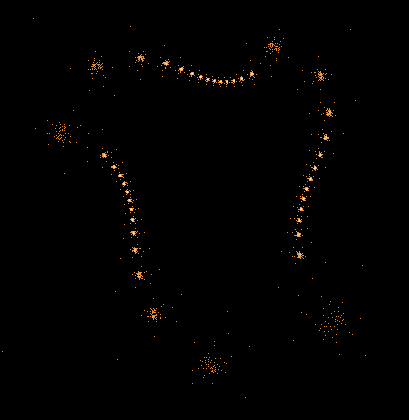
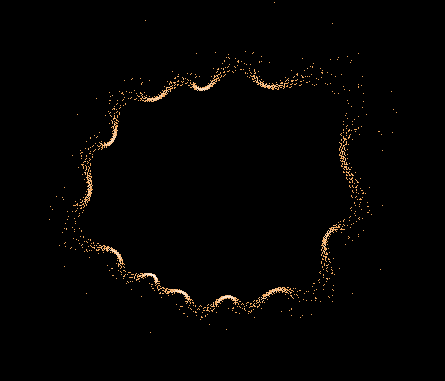
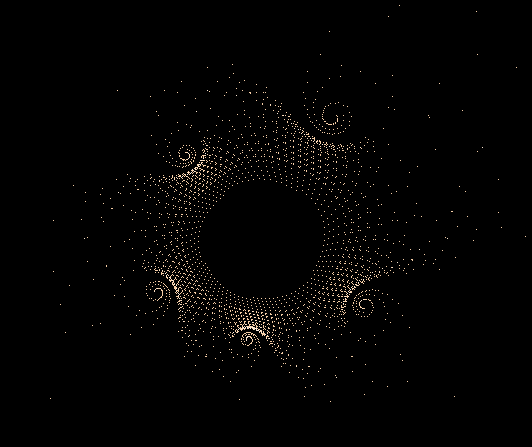

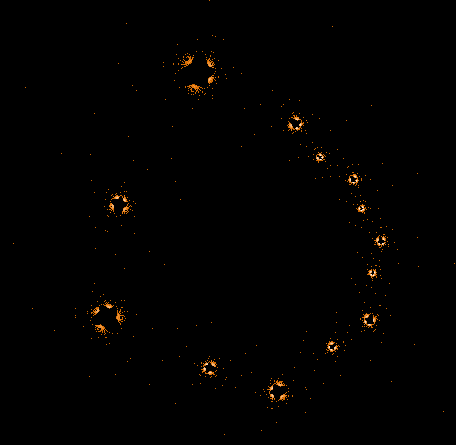
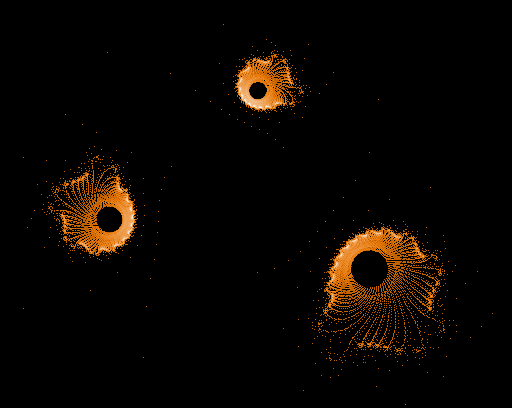
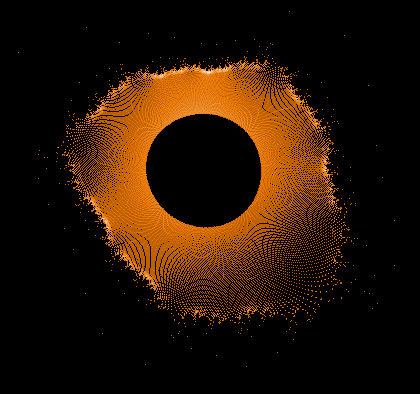
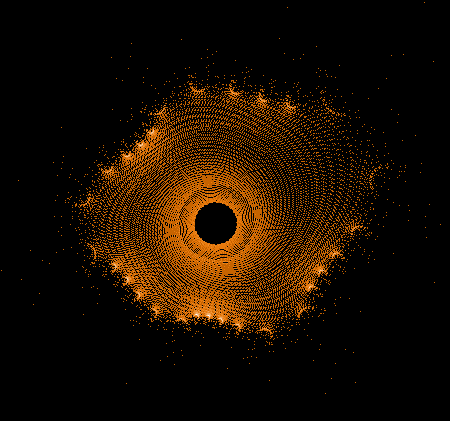
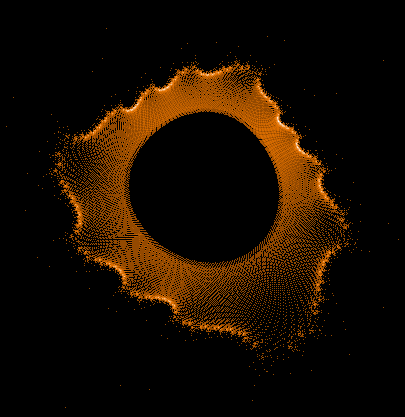

- Serie 1 -
100...1.000.000 Iterationen, 1.000.000 Z-Bahnen
Gesamtbild (Histogramm verbessert)
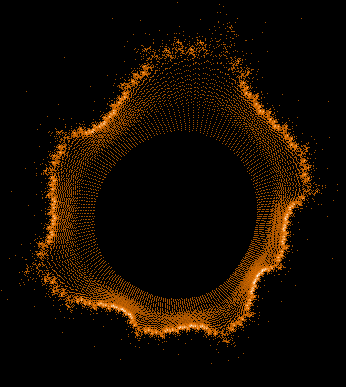
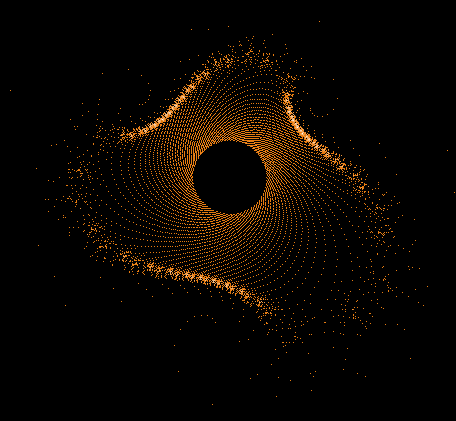
Einige einzelne Z-Bahnen aus obigen Gesamtbild
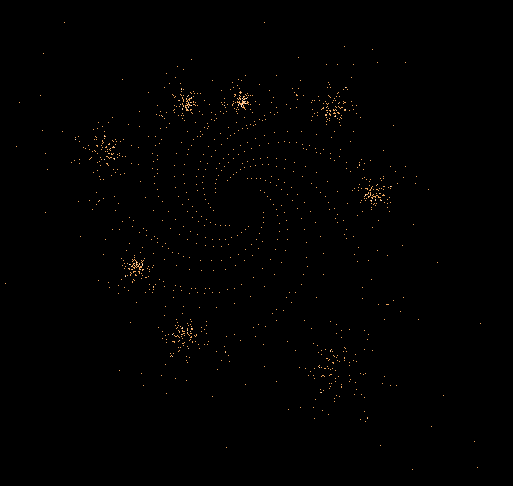
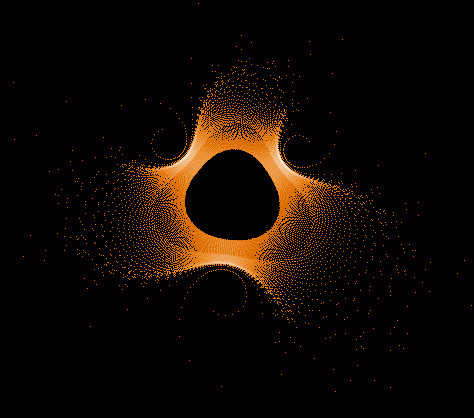
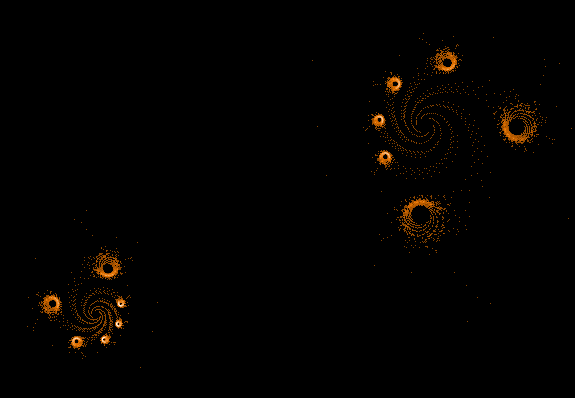
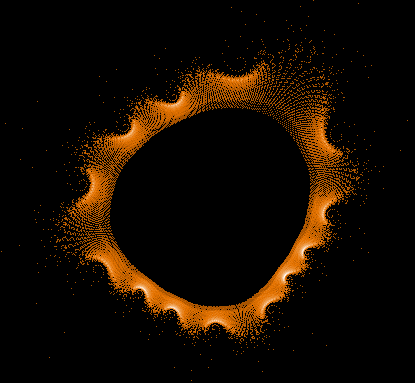

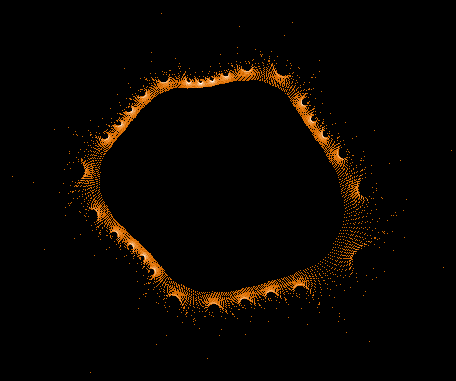
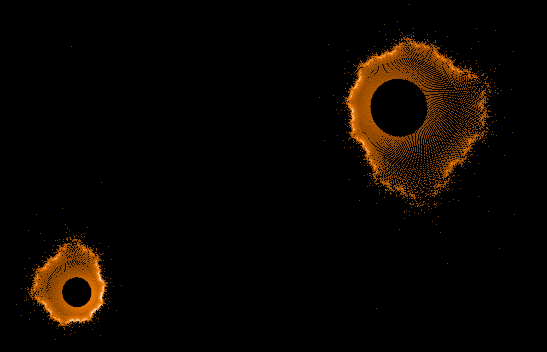
Quelle: